Average Rate of Change Calculator is an average measure of change given a function, over an interval. It’s the total change of the output of the function isolated by the change in the function’s input.
To find the rate of change, first characterize the function that you’ll use to calculate it, along with an interval [a, b].
Then, you can find the average rate of change utilizing the slant formula. The average rate of change is actually a slant, yet rather than a linear incline where the average between two focuses is decreased to nothing, a function is utilized.
The Average Calculator is here to assist you with understanding the straightforward idea taken cover behind a long, tad confounding name. What is the rate of change?
Generally speaking, it shows the relationship between two factors. Search for a more precise average rate of change definition beneath. We will also demonstrate and explain the average rate of change formula with two or three examples of how to utilize it.
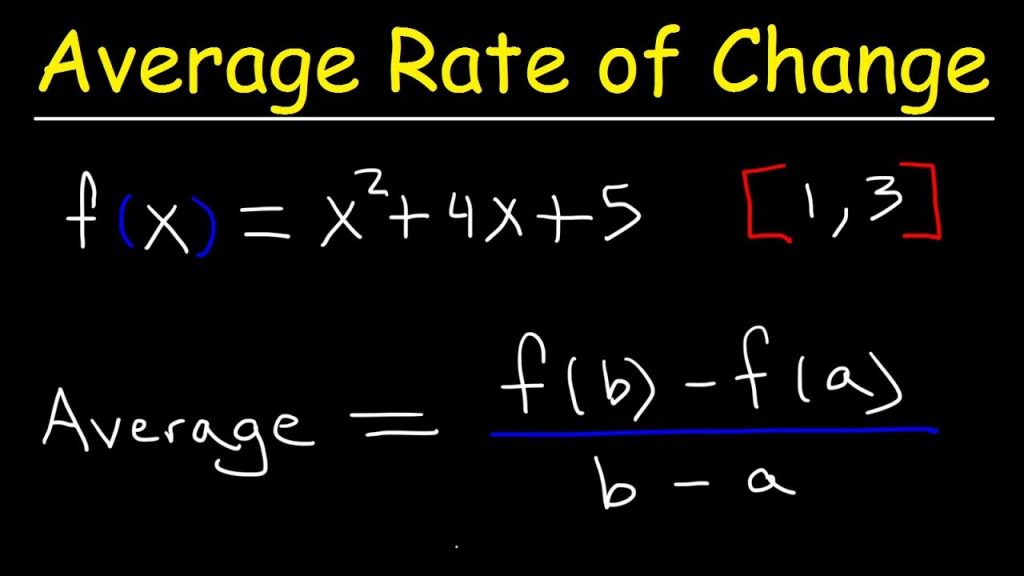
What is rate of change? – the average rate of change definition
All that continues to move. Change is inevitable. Minus GST on Calculator Starting with the acceleration of your bicycle or car, through to population development, from the blood stream in your veins to the symbiosis of your cells, the rate of change allows us to establish the value associated with those changes.
The average rate of change is a rate that portrays how one number changes, on average, in relation to another. On the off chance that you have a function, it is the incline of the line drawn between two focuses. However, don’t mistake it for slant. You can involve the average rate of change for any given function, not just linear ones.
Average rate of change formula
In the accompanying picture, we marked two focuses to assist you with better understanding how to find the average rate of change.
On the off chance that it’s sure, it means that one coordinate increases as the other also increases. For example, the more you ride a bicycle, the more calories you consume.
It’s equal to zero when one coordinate changes, yet the other one does not. A genuine example may be not reading up for your exams. As time starts expiring, the amount of things to learn doesn’t change.
The average rate of change is negative when one coordinate increases while the other one decreases. Suppose you’re going on a vacation. The additional time you spend on your travel, the nearer you are to your destination.
How to find the average rate of change? – first example
We should calculate the average rate of change of distance (average speed) of a train going from Paris to Rome (1420,6 km). On the accompanying chart you can see the change in distance after some time:
As you see, the speed wasn’t constant. The train stopped twice, in the middle between stops, it went significantly more slow. Yet, for calculating the average speed, the main variables that matter are the change in distance and the change in time.
How Average Rate of Change Calculator Works?
Input:
- Firstly, enter a function for calculating the average rate.
- Presently, plug in the values of the interval
- Press the calculate button
Output:
- Initially, the calculator displays the given function and interval.
- Then, give the stepwise arrangement.
- Thus, you can do calculations various times by click on the “Recalculate” button.
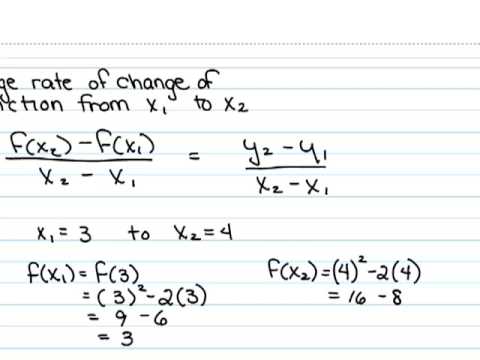
How do you calculate the rate of change of a function?
It’s actually easier to calculate the integral of a function than the derivative of it; the integral of a function between two focuses (a,b) is always obvious in the event that f is piecewise nonstop among an and b, however the derivative need not be clear cut over the range. Work Out GST on Calculator For example, think about the function:
So I suspect you’re asking why the anti-derivative (also, misleadingly, called the endless integral) is hard to register. The answer is that the derivative is a local property of a function (the incline of the tangent to the function at each point); where it is distinct it’s easy to register. We should take a gander at the mathematical definitions of the derivative and anti-derivative.
Obviously the definition of the derivative also lets us know how to figure the derivative; yet the definition of the anti-derivative gives us no assistance at all in finding the anti-derivative, and without a doubt it’s easy to find smooth, ceaseless functions wherever characterized that have no shut structure anti-derivative.
How do you find the average rate of change from a graph?
To make this instinctive, lets say that you are driving from Alexandria to Cairo. It took you 3 hours to reach your destination, yet for one hour of this 3 hours you stopped at a rest to share a meal with your family. The average speed in this hour was zero, however the average speed accross the 3 hours was most certainly not zero.
Therefore while calculating the average rate, the range should be determined in the inquiry. Lets say you want to find the average rate between point (x1,y1) and point (x2,y2). What you are gonna do, regardless of the type of the graph you have is to interface those two focuses together, and calculate the incline of the line. The incline of the line is equal to the average rate accross the predefined domain from x1 to x2.
This is because the idea of average deals with constant equivalencies. It is the “as if” idea. You traveling from Alexandria to Cairo in 3 hours at 140 km/hr at constant speed however stopped for one hour is as on the off chance that you traveled for 3 hours at a constant speed of 100km/hr ceaselessly. The main goal is to sort out equivalent constants, that do the work.
Graph theory is the mathematical investigation of associations between things. This is formalized through the thought of hubs (any sort of substance) and edges (relationships between hubs). There is an idea of undirected graphs, wherein the edges are symmetric, and coordinated graphs, where the edges are not symmetric (see examples underneath). Some of the time the graph is weighted: you can assign numeric values to the edges to indicate which relationships are more grounded or more expensive than others.
















Leave a Reply